DeadChannel

When did Pet_Sounds disable his account?

grindy

About two weeks ago.

__________________
A smell of petroleum prevails throughout.

DeadChannel

Anyone know why?

Zhanteimi

He asked that it be disabled.

Pet_Sounds

When I'm bored, I like to fiddle around with math and science. I try to teach myself tricky concepts. Earlier this week it was special relativity. Here's something I tackled a few months ago. Enjoy.


In mathematics, certain numbers are important. They have special properties, and they seem to pop up everywhere. Five in particular stand out: 0, 1, i, π, and e. These five can be related in a mathematician's wet dream: Euler's formula.



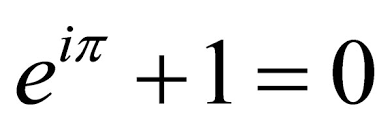
It has each of the big five mathematical constants, an addition, a multiplication, and an exponent. It's simple and elegant. It's beautiful. It's mind-blowing.

It would be tempting to go down a rabbit hole and start breaking down the history and meaning of each of the components of this equation. However, such an explanation would be incredibly technical, and I doubt anybody on a music forum would be interested in reading it. Instead, I'm going to explain why Euler's identity works, in a way that (hopefully) anyone who knows basic math can understand. There's a much quicker, more elegant way to prove it using calculus, but all you need for this explanation is algebra. Trigonometry is a bonus.

I guess I should provide a little background about each number. e is approximately 2.17828. It has a bunch of special properties that make it very important. i is an imaginary number, the square root of -1. It doesn't exist in the real world, since no number multiplied by itself can be negative. (Think about it: positive × positive = positive, negative × negative = positive, zero × zero = zero.) However, it's useful for manipulating equations—eventually, all the i's end up as i²'s and can be replaced with -1's. Electrical engineers use it in calculations involving alternating current, among other things. π is a circle's circumference (perimeter) divided by its diameter (the distance across). Hence the equation circumference = 2πr. (r is the half the diameter, or the radius, of a circle.) I don't need to explain 1 and 0.

We can express numbers such as π and e, which have an infinite number of decimal places, as the sum of an infinite series. e is the sum of 1/0! + 1/1! + 1/2! + 1/3! ... The ellipsis points mean the numbers go on and on, following that pattern. The exclamation points denote "factorial." 3! = 3 × 2 × 1, 4! = 4 × 3 × 2 × 1, etc. Don't worry too much about the factorial concept, it's not important in this discussion. The important thing is that we can accurately express a number as the sum of an infinite series, called a "Taylor series."

It turns out that e^x (alas, no easy superscripts on MB) can be expressed as the sum of the infinite series x^0/0! + x^1/1! + x^2/2! + x^3/3! ... We can substitute any number for x. To find the series for e², we would plug 2 into that equation. So, we plug in the number ix, which is not the Roman numeral for 9, but the imaginary number i times any number x. This leaves us with the following expression:

e^ix = (ix)^0/0! + (ix)^1/1! + (ix)^2/2! + (ix)^3/3! + (ix^4)/4! + (ix)^5/5! + (ix)^6/6! + (ix)^7/7! + (ix)^8/8! ...

Which we can simplify by multiplying (ix)² = (ix)(ix) = i²x² Oh yeah, in algebra, because use the letter x, we usually do away with multiplication signs. If two letters are written back to back or with • in between them, that means they're being multiplied. Anyway, that series simplifies to

e^ix = 1 + ix + i^2x^2/2! + i^3x^3/3! + i^4x^4/4! + i^5x^5/5! + i^6x^6/6! + i^7x^7/7! + i^8x^8/8! ...

We can replace every i² with -1. Thus, i^3= -i, i^4 = 1, i^5 = i, i^6 = -1, i^7 = -i, and x^8 = 1.

e^ix = 1 + ix - x^2/2! - ix^3/3! + x^4/4! + ix^5/5! - x^6/6! - ix^7/7! + x^8/8! ...

Now it's time to leave that series and move on to some basic trigonometry.



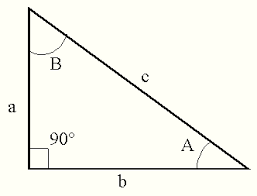
Just remember that the sine of angle A is a/c and the cosine of angle A is b/c. These ratios can be calculated for any angle. It turns out that the cosine of 180° is -1 and the sine of 180° is 0. Remember this.

Sine and cosine (sin and cos) can also be expressed as infinite series. We write sin x to mean "the sine of an angle measuring x."

It turns out that

cos x = 1 - x^2/2! + x^4/4! - x^6/6! + x^8/8! ...

Aha! We can plug that value into the series for e^ix, leaving us with

e^ix = cos x + (ix - ix^3/3! + ix^5/5! - ix^7/7! ...)

It also turns out that

sin x = x - x^3/3! + x^5/5! - x^7/7! ...

We multiply everything by i:

i sin x = ix - ix^3/3! + ix^5/5! - ix^7/7! ...

Voila! We plug that value into the other series and get

e^ix = cos x + i sin x

To get Euler's formula, we let x equal π.

e^iπ = cos π + i sin π

Now, I must introduce one more thing. You're probably used to seeing angles measured in degrees. Mathematicians like to measure them in radians, a dimensionless unit where π = 180°. Remember how I said earlier that the cosine of 180° is -1 and the sine of 180° is 0? Well, that means that the cosine and sine of π are also -1 and 0. Plug these values in and we get something that looks like this:

e^iπ = -1 + i • 0

Zero times anything is zero, so

e^iπ = -1

We rearrange to get



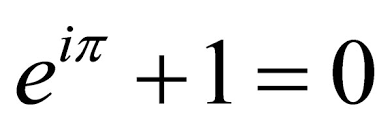
Why am I posting this on a music forum?

__________________
Everybody's dying just to get the disease

Pet_Sounds

I hear the drums echoing tonight, but she hears only whispers of some quiet conversation.
She's coming in 12:30 flight. The moonlit wings reflect the stars that guide me toward salvation.
I stopped an old man along the way, hoping to find some old forgotten words or ancient melodies
He turned to me as if to say,
"Hurry boy, it's waiting there for you..."

IT'S GONNA TAKE A LOT TO DRAG ME AWAY FROM YOU
THERE'S NOTHING THAT A HUNDRED MEN OR MORE COULD EVER DO
I BLESS THE RAINS DOWN IN AFRICA
GONNA TAKE SOME TIME TO DO THE THINGS WE NEVER HAVE

You get the idea, right?

There's something special about that song ("Africa" by Toto, for the unenlightened). You know those pieces of music that inspire feelings you can't quite articulate? That appeal to something you can never express in writing? "Africa" is one of them. It's wild, peaceful, jubilant, and melancholy all at once. It's the perfect song for when you're upset, when you're working out, when you're falling asleep, when you're in love, when you're... I can't explain it—just listen.



I think I'm hearing the sound of freedom.

__________________
Everybody's dying just to get the disease

Mondo Bungle

that's what yo girl said

__________________

Pet_Sounds

Three Quotations From One of My Favourite People

Richard Feynman



Probably the most recognizable scientist after Einstein. Shared the 1965 Nobel Prize in Physics for his work on quantum electrodynamics. Also a musician, painter, and safecracker.

"Physics is like sex: sure, it may give some practical results, but that's not why we do it."

"Philosophy of science is about as useful to scientists as ornithology is to birds."

"Study hard what interests you in the most undisciplined, irreverent and original manner possible."

To be continued...

__________________
Everybody's dying just to get the disease

Pet_Sounds

https://youtu.be/SUFSB2plwzM

In memory of Audrey W.
2001-2017

"You expected to be sad in the fall. Part of you died each year when the leaves fell from the trees and their branches were bare against the wind and the cold, wintery light. But you knew there would always be the spring, as you knew the river would flow again after it was frozen. When the cold rains kept on and killed the spring, it was as though a young person died for no reason."


"Everyone must leave something behind when he dies, my grandfather said. A child or a book or a painting or a house or a wall built or a pair of shoes made. Or a garden planted. Something your hand touched some way so your soul has somewhere to go when you die, and when people look at that tree or that flower you planted, you're there.

"It doesn't matter what you do, he said, so long as you change something from the way it was before you touched it into something that's like you after you take your hands away. The difference between the man who just cuts lawns and a real gardener is in the touching, he said. The lawn-cutter might just as well not have been there at all; the gardener will be there a lifetime."


I'll never know what anguish you went through, or what led you to take that final, irreversible step. Perhaps it's best that way.

Farewell, my friend. My only regret is that we didn't have more time together. Thank you for touching my life.

With love,

Spencer

__________________
Everybody's dying just to get the disease

Tristan_Geoff

My condolences, however meaningless they may be. You and her other friends and family didn't deserve this, and she didn't deserve whatever she was going through.

__________________
YW Fam: All MB Music Projects Under One Roof

Emo/Pop Punk Journal

Techno Journal